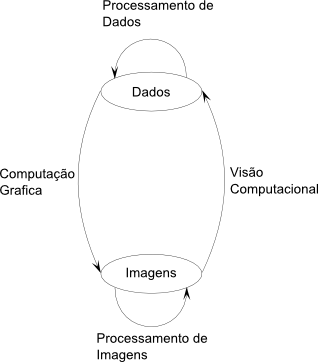
Computação Gráfica

CG é uma área da computação dedicada a criação, armazenamento e manipulação de imagens baseada em modelos matemáticos.

Lecture 1

Iniciaremos nosso curso aprendendo como construir uma imagem.

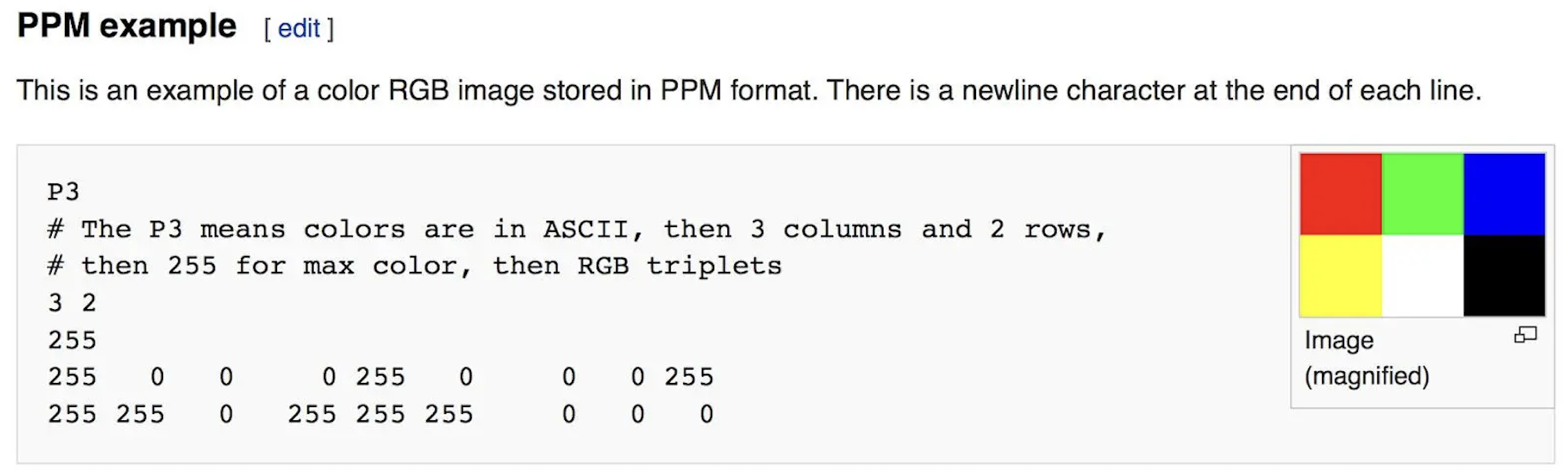
Portable Pixel Map (PPM)

O formato PPM nasceu no final da década de $80$ para compartilhar imagens facilmente entre diferentes plataformas.

Figure 1. Definição da Wikipedia

Código

Podemos escrever um código em C para construir uma imagem usando o formato PPM. Este objetivo será alcançado através da análise do programa ppm_create.c.

Figure 2. Imagem PPM construída a partir do código "ppm_create.c"

/**
 * \file ppm_create.c
 *
 * \brief Criacao de uma imagem em PPM.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date April 2025
 */

#include <stdio.h>

int main(){

  // dimensoes da imagem
  int width = 256;
  int height = 256;

  // Configurando o header do formato PPM
  printf("P3\n %d \t %d\n 255\n", width, height);

  for (int i = 0; i < height; i++){ // Altura
    for (int j = 0; j < width; j++){ // Largura
      printf("%d \t %d \t %d \n", i, j, 63);
    }
  }

  return 0;
}

Descrição do programa

Inserimos na primeira linha do arquivo a biblioteca para lidar com entrada/saída de dados na linguagem C.

#include <stdio.h>

Definimos as dimensões (largura e altura) da imagem que estamos construindo.

int width = 256;
int height = 256;

Em seguida, configuramos o cabeçalho do formato PPM.

printf("P3\n %d \t %d\n 255\n", width, height);

No laço de repetição, percorremos a largura e altura da imagem preenchendo as cores dos pixels.

for (int i = 0; i < height; i++){ // Altura
    for (int j = 0; j < width; j++){ // Largura
      printf("%d \t %d \t %d \n", i, j, 63);
    }
}

Compilação

O processo de compilação é realizado através do compilador GCC através do seguinte comando:

gcc <nome_arquivo>.c -o <nome_executavel>

Este comando criará um arquivo executável e a saída deve ser direcionada para um arquivo com extensão ".ppm".

./<nome_executavel> > output.ppm

Exercício

Construa uma imagem $100 \times 100$ usando o formato PPM com fundo preto que tem apenas 1 pixel vermelho no centro da imagem.
Implemente uma função que altera o valor de um pixel da imagem.
Codifique uma função que salva a imagem no formato PPM.
Crie uma função que inicializa uma imagem com branco.
Construa uma imagem $100 \times 100$ usando o formato PPM com fundo preto e escreva o caractere ' T ' no centro da imagem com alto contraste em relação ao fundo da imagem.

Lecture 2

Nesta parte da disciplina aprenderemos como renderizar um segmento de reta usando as equações vetoriais.

Segmento de reta

Sejam $A = (x_0, y_0, z_0)$ e $B = (x_1, y_1, z_1)$ dois pontos do espaço. Podemos traçar uma equação da reta entre esses dois pontos usando a equação: $r(t) = A + t( B - A)$, onde $t \in [0, 1$].

Figure 3. Segmento de reta

Código

O algoritmo de renderização do segmento de reta está disponível no arquivo linesegment.c.

/**
 * \file linesegment.c
 *
 * \brief Implementação do segmento de reta usando equacoes vetoriais.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date May 2025
 */

#include <stdio.h>

#define width 200
#define height 200

unsigned char image[height][width][3];

// Funcao para preencher um pixel na imagem
void putPixel( int x, int y, unsigned char r, unsigned char g, unsigned char b){
  if (( x >= 0 ) && ( x <= width )  && ( y >= 0 ) && ( y <= height )){
    image[x][y][0] = r;
    image[x][y][1] = g;
    image[x][y][2] = b;
  }
}

// Funcao para limpar a imagem
void clearImage(){
  for (int y = 0; y < height; y++)
    for (int x = 0; x < width; x++)
      putPixel(x, y, 255, 255, 255);
}

// Funcao para salvar imagem no formato PPM
void saveImage(){
  // Configurando o header do formato PPM
  printf("P3\n %d \t %d\n 255\n", width, height);

  for (int y = 0; y < height; y++){ // Altura
    for (int x = 0; x < width; x++){ // Largura
      for (int c = 0; c < 3; c++){ // Canal: r, g, b
        printf("%d \t", image[x][y][c]);
      }
      printf("\n");
    }
  }
}

// Algoritmo do Segmento de Reta
void drawLine( int x0, int y0, int x1, int y1 ){
  for (float t = 0.0; t < 1.0; t = t + 0.001){
    putPixel((int)(x0 + (x1 - x0)*t), (int)(y0 + (y1 - y0)*t), 255, 0, 0 );
  }
}

int main(){

  // Limpar a imagem
  clearImage();

  // Executar o algoritmo
  drawLine(0, 0, 200, 200);

  // Salvar a imagem em PPM
  saveImage();

  return 0;
}

Descrição do programa

Iniciamos nosso programa incluindo a biblioteca padrão da linguagem C para gerar entrada/saída de dados.

#include <stdio.h>

Após a declaração da biblioteca, definimos globalmente as dimensões da imagem e a variável da imagem como um array multidimensional que armazena valores de 8 bits sem sinal.

#define width 200
#define height 200

unsigned char image[height][width][3];

Posteriormente, declarei algumas funções úteis para manipulação da imagem. A primeira delas é a função para setar um pixel na imagem.

void putPixel( int x, int y, unsigned char r, unsigned char g, unsigned char b){
  if (( x >= 0 ) && ( x <= width )  && ( y >= 0 ) && ( y <= height )){
    image[x][y][0] = r;
    image[x][y][1] = g;
    image[x][y][2] = b;
  }
}

A segunda função é necessária para preencher a imagem com uma cor de fundo.

void clearImage(){
  for (int y = 0; y < height; y++)
    for (int x = 0; x < width; x++)
      putPixel(x, y, 255, 255, 255);
}

Por fim, a última função é responsável por salvar o array multidimensional em formato PPM.

void saveImage(){
  // Configurando o header do formato PPM
  printf("P3\n %d \t %d\n 255\n", width, height);

  for (int y = 0; y < height; y++){ // Altura
    for (int x = 0; x < width; x++){ // Largura
      for (int c = 0; c < 3; c++){ // Canal: r, g, b
        printf("%d \t", image[x][y][c]);
      }
      printf("\n");
    }
  }
}

O algoritmo de renderização do segmento de reta é implementado em seguida.

void drawLine( int x0, int y0, int x1, int y1 ){
  for (float t = 0.0; t < 1.0; t = t + 0.001){
    putPixel((int)(x0 + (x1 - x0)*t), (int)(y0 + (y1 - y0)*t), 255, 0, 0 );
  }
}

Renderização de modelos 3D

O formato .obj (Wavefront OBJ) é um padrão amplamente utilizado para representar modelos 3D de forma simples e legível. Ele armazena informações sobre vértices (v), normais (vn), texturas (vt) e faces (f), onde cada face é formada por índices que referenciam os vértices previamente definidos. As faces podem ser triangulares ou poligonais e podem incluir referências opcionais a coordenadas de textura e normais no formato f v/vt/vn.

Figure 4. Modelo tridimensional gerado a partir da renderização em wireframe

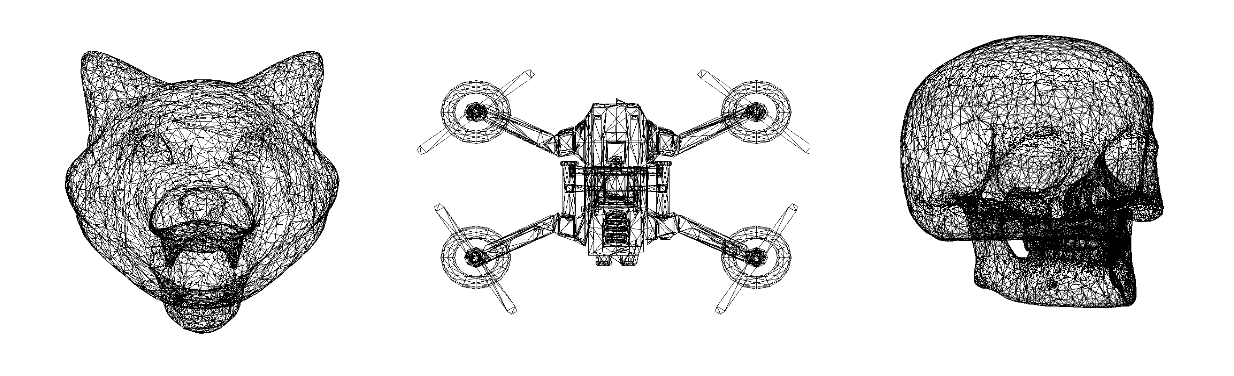
O processo de renderização do modelo 3D exige arquivos .obj adquiridos livremente no domínio free3d.com. Os modelos utilizados na imagem acima foram wolf.obj, drone.obj e cranio.obj.

Código

A implementação do código de renderização 3D é realizada através dos arquivos: model.h que contém todos os protótipos de funções que serão úteis para manipulação dos modelos 3D, model.c é o arquivo que contém as implementações das funções de manipulação dos modelos 3D e wireframe.c que realiza a execução das funções implementadas.

/**
 * \file model.h
 *
 * \brief Header com protótipos de funções para manipulação de modelo 3D.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date May 2025
 */

#ifndef MODEL_H
#define MODEL_H

#define WIDTH 800
#define HEIGHT 800
#define MAX_VERTICES 50000
#define MAX_FACES 50000
#define MAX_FACE_VERTS 32

typedef struct {
  float x, y, z;
} Vertex;

typedef struct {
  int verts[MAX_FACE_VERTS];
  int n;
} Face;

unsigned char image[HEIGHT][WIDTH][3];

void set_pixel(int x, int y, unsigned char r, unsigned char g, unsigned char b);

void clr();

void save();

void draw_line(int x0, int y0, int x1, int y1);

int load_obj(const char *filename, Vertex *vertices, int *vcount, Face *faces, int *fcount);

void resizing( Vertex v0, Vertex v1 );

void render_faces(Vertex *vertices, Face *faces, int vcount, int fcount);


#endif

/**
 * \file model.c
 *
 * \brief Implementação das funções de manipulação do modelo 3D.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date May 2025
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>

#include "model.h"

void set_pixel(int x, int y, unsigned char r, unsigned char g, unsigned char b) {
  if (x >= 0 && x < WIDTH && y >= 0 && y < HEIGHT) {
    image[y][x][0] = r;
    image[y][x][1] = g;
    image[y][x][2] = b;
  }
}

void draw_line(int x0, int y0, int x1, int y1) {
  for (float t = 0.0; t < 1.0; t = t + 0.0001)
    set_pixel((int)x0+(x1-x0)*t, (int)y0+(y1-y0)*t, 0, 0, 0);
}

void clr(){
  for(int i = 0; i < WIDTH; i++)
    for(int j = 0; j < HEIGHT; j++)
      for(int c = 0; c < 3; c++)
        image[i][j][c] = 255;
}

void save(){
  printf("P3\n %d \t %d\n 255\n", WIDTH, HEIGHT);
  for(int i = 0; i < WIDTH; i++){
    for(int j = 0; j < HEIGHT; j++){
      for(int c = 0; c < 3; c++){
        printf("%d \t", image[i][j][c]);
      }
      printf("\n");
    }
  }
}

int load_obj(const char *filename, Vertex *vertices, int *vcount, Face *faces,
             int *fcount) {
    FILE *file = fopen(filename, "r");
    if (!file) {
        perror("Erro ao abrir o arquivo");
        return 0;
    }

    char line[512];
    *vcount = 0;
    *fcount = 0;

    while (fgets(line, sizeof(line), file)) {
        if (strncmp(line, "v ", 2) == 0) {
            if (sscanf(line + 2, "%f %f %f", &vertices[*vcount].x,
                       &vertices[*vcount].y, &vertices[*vcount].z) == 3) {
                (*vcount)++;
            }
        } else if (strncmp(line, "f ", 2) == 0) {
            Face face = {.n = 0};
            char *token = strtok(line + 2, " \n");
            while (token && face.n < MAX_FACE_VERTS) {
                int index;
                if (sscanf(token, "%d", &index) == 1) {
                    face.verts[face.n++] = index;
                }
                token = strtok(NULL, " \n");
            }
            faces[(*fcount)++] = face;
        }
    }

    fclose(file);
    return 1;
}

void resizing( Vertex v0, Vertex v1 ){
  int x0 = (int)((v0.x + 1.0f) * WIDTH / 2.0f);
  int y0 = (int)((1.0f - v0.y) * HEIGHT / 2.0f);
  int x1 = (int)((v1.x + 1.0f) * WIDTH / 2.0f);
  int y1 = (int)((1.0f - v1.y) * HEIGHT / 2.0f);

  draw_line(x0, y0, x1, y1);
}


void render_faces(Vertex *vertices, Face *faces, int vcount, int fcount) {
    for (int i = 0; i < fcount; i++) {
        Face face = faces[i];
        for (int j = 0; j < face.n; j++) {
            Vertex v0 = vertices[face.verts[j] - 1];
            Vertex v1 = vertices[face.verts[(j + 1) % face.n] - 1];
            resizing(v0, v1);
        }
    }
}

/**
 * \file wireframe.c
 *
 * \brief Implementação do arquivo principal de renderização do modelo 3D.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date May 2025
 */

#include "model.h"

int main() {
    Vertex vertices[MAX_VERTICES];
    Face faces[MAX_FACES];
    int vcount, fcount;

    clr();

    // Lê o arquivo OBJ enviado
    if (!load_obj("models/cranio.obj", vertices, &vcount, faces, &fcount)) {
        return 1;
    }

    // Renderiza as faces no framebuffer
    render_faces(vertices, faces, vcount, fcount);

    save();

    return 0;
}

Compilação

O processo de compilação é realizado através do compilador GCC através do seguinte comando:

gcc <nome_arquivo>.c <nome_biblioteca>.c -o <nome_executavel>

Este comando criará um arquivo executável e a saída deve ser direcionada para um arquivo com extensão ".ppm".

./<nome_executavel> > output.ppm

Exercício

Estudar o código acima substituindo o modelo.
Substitua o modelo usado no código por robot.obj.
Implemente uma função para exibir apenas os pontos (nuvem de pontos) ao invés do arramado (veja imagem abaixo).

Figure 5. Nuvem de pontos gerados a partir de um modelo 3D.

Aplique as transformações estudadas no modelo $3D$.

Lecture 3

Digital Differential Analyze (DDA)

Algoritmo clássico de rasterização de linhas. Este algoritmo utiliza a equação da reta para gerar pontos de uma linha entre dois pontos $(x_{0}, y_{0})$ e $(x_{1}, y_{1})$, incrementando em intervalos fixos.

Figure 6. Linha gerada pelo algoritmo DDA

Código

A implementação do algoritmo DDA (disponível no arquivo dda.c) exige conhecimento prévio de alguns detalhes matemáticos da equação da reta.

/**
 * \file dda.c
 *
 * \brief Implementação do algoritmo DDA.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date April 2025
 */

#include <stdio.h>
#include <stdlib.h> // abs

#define width 200
#define height 200

unsigned char image[height][width][3];

// Funcao para preencher um pixel na imagem
void putPixel( int x, int y, unsigned char r, unsigned char g, unsigned char b){
  if (( x >= 0 ) && ( x <= width )  && ( y >= 0 ) && ( y <= height )){
    image[x][y][0] = r;
    image[x][y][1] = g;
    image[x][y][2] = b;
  }
}

// Funcao para limpar a imagem
void clearImage(){
  for (int y = 0; y < height; y++)
    for (int x = 0; x < width; x++)
      putPixel(x, y, 255, 255, 255);
}

// Funcao para salvar imagem no formato PPM
void saveImage(){
  // Configurando o header do formato PPM
  printf("P3\n %d \t %d\n 255\n", width, height);

  for (int y = 0; y < height; y++){ // Altura
    for (int x = 0; x < width; x++){ // Largura
      for (int c = 0; c < 3; c++){ // Canal: r, g, b
        printf("%d \t", image[x][y][c]);
      }
      printf("\n");
    }
  }
}

// Algoritmo DDA
void drawDDA( int x0, int y0, int x1, int y1 ){
  // calcula a variacao
  int dx = x1 - x0;
  int dy = y1 - y0;

  // calcula o número de passos de incremento
  int steps = abs(dx) > abs(dy) ? abs(dx) : abs(dy);

  // define o incremento em cada eixo
  float x_inc = (float) dx / steps;
  float y_inc = (float) dy / steps;

  float x = x0;
  float y = y0;

  for (int i = 0; i <= steps; i++){
    putPixel((int)x, (int)y, 255, 0, 0);
    x += x_inc;
    y += y_inc;
  }
}

int main(){

  // Limpar a imagem
  clearImage();

  // Executar o algoritmo DDA
  drawDDA(0, 0, 200, 200);

  // Salvar a imagem em PPM
  saveImage();

  return 0;
}

Descrição do programa

Iniciamos o código inserindo a biblioteca padrão de entrada/saída de dados da linguagem C e a biblioteca stdlib.h para obter o módulo de um número.

#include <stdio.h>
#include <stdlib.h> // abs

Após inserir as bibliotecas, optei por definir globalmente as dimensões da imagem e a própria imagem como um array multidimensional do tipo caractere sem sinal para representar cada canal de cor com 8 bits.

#define width 200
#define height 200

unsigned char image[height][width][3];

Posteriormente, codifiquei algumas funções que serão úteis para manipular as imagens PPM. A primeira função foi para setar um valor de cor para um pixel.

void putPixel( int x, int y, unsigned char r, unsigned char g, unsigned char b){
  if (( x >= 0 ) && ( x <= width )  && ( y >= 0 ) && ( y <= height )){
    image[x][y][0] = r;
    image[x][y][1] = g;
    image[x][y][2] = b;
  }
}

A segunda função que implementei que nos ajudará é a função para preencher com branco toda a imagem.

void clearImage(){
  for (int y = 0; y < height; y++)
    for (int x = 0; x < width; x++)
      putPixel(x, y, 255, 255, 255);
}

Por fim, codifiquei uma função específica para salvar o array multidimensional no formato PPM.

void saveImage(){
  // Configurando o header do formato PPM
  printf("P3\n %d \t %d\n 255\n", width, height);

  for (int y = 0; y < height; y++){ // Altura
    for (int x = 0; x < width; x++){ // Largura
      for (int c = 0; c < 3; c++){ // Canal: r, g, b
        printf("%d \t", image[x][y][c]);
      }
      printf("\n");
    }
  }
}

O algoritmo DDA é implementado seguindo os seguintes passos:

Calcular o valor de variação nos eixos x e y;
Encontra a maior variação e adota ela como número de passos do algoritmo;
Define o incremento em cada eixo;
Pinta do ponto inicial até o ponto final incrementando os incrementos em cada eixo.

void drawDDA( int x0, int y0, int x1, int y1 ){
  // calcula a variacao
  int dx = x1 - x0;
  int dy = y1 - y0;

  // calcula o número de passos de incremento
  int steps = abs(dx) > abs(dy) ? abs(dx) : abs(dy);

  // define o incremento em cada eixo
  float x_inc = (float) dx / steps;
  float y_inc = (float) dy / steps;

  float x = x0;
  float y = y0;

  for (int i = 0; i <= steps; i++){
    putPixel((int)x, (int)y, 255, 0, 0);
    x += x_inc;
    y += y_inc;
  }
}

Análise do algoritmo DDA

Table 1. Avaliando vantagens e desvantagens do algoritmo DDA
Vantagens	Desvantagens
Simples de implementar	Usa ponto flutuante
Funciona em qualquer inclinação	Pode causar acúmulo de erros de arredondamento

Exercícios

Implemente uma função que os argumentos são os pontos de um polígono convexo e o retorno é uma imagem PPM.
Edite o código de renderização de modelos 3D para usar o algoritmo DDA.
Utilize a biblioteca time.h da linguagem C e verifique o tempo de execução do algoritmo que utiliza equações vetoriais e DDA.

Lecture 4

Bresenham

Jack Bresenham propôs em 1965 no artigo Algorithm for Computer Control of a Digital Plotter um algoritmo de rasterização de linhas com tipo inteiro. No texto Bresenham’s Algorithm contém uma breve explicação sobre o algoritmo.

Figure 7. Linhas gerada pelo algoritmo de Bresenham

Código

A implementação do algoritmo de Bresenham está disponível no arquivo bresenhamLines.c.

/**
 * \file bresenhamLines.c
 *
 * \brief Implementação do algoritmo bresenham para linhas.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Árido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date April 2025
 */

#include <stdio.h>
#include <stdlib.h> // abs

#define width 200
#define height 200

unsigned char image[height][width][3];

// Funcao para preencher um pixel na imagem
void putPixel( int x, int y, unsigned char r, unsigned char g, unsigned char b){
  if (( x >= 0 ) && ( x <= width )  && ( y >= 0 ) && ( y <= height )){
    image[x][y][0] = r;
    image[x][y][1] = g;
    image[x][y][2] = b;
  }
}

// Funcao para limpar a imagem
void clearImage(){
  for (int y = 0; y < height; y++)
    for (int x = 0; x < width; x++)
      putPixel(x, y, 255, 255, 255);
}

// Funcao para salvar imagem no formato PPM
void saveImage(){
  // Configurando o header do formato PPM
  printf("P3\n %d \t %d\n 255\n", width, height);

  for (int y = 0; y < height; y++){ // Altura
    for (int x = 0; x < width; x++){ // Largura
      for (int c = 0; c < 3; c++){ // Canal: r, g, b
        printf("%d \t", image[x][y][c]);
      }
      printf("\n");
    }
  }
}

// Algoritmo Bresenham (1º quadrante)
void drawBresenhamLinesIncomplete( int x0, int y0, int x1, int y1 ){

  // calcula a variacao
  int dx = x1 - x0;
  int dy = y1 - y0;

  // calcula o erro
  int D = (2 * dy) - dx;

  int x = x0;
  int y = y0;

  putPixel(x, y, 255, 0, 0);

  while (x < x1){
    x = x + 1;
    if ( D < 0 ){
      D = D + (2 * dy);
    }
    else{
      y = y + 1;
      D = D + (2 * ( dy - dx ));
    }
    putPixel(x, y, 255, 0, 0);
  }

}

// Algoritmo Bresenham ( todos os quadrantes )
void drawBresenhamLines( int x0, int y0, int x1, int y1 ){
  // calcula a variacao absoluta
  int dx = abs(x1 - x0);
  int dy = abs(y1 - y0);

  // indica a direcao da reta
  int sx = (x0 < x1) ? 1 : -1; // direção de x
  int sy = (y0 < y1) ? 1 : -1; // direção de y

  // calcula o erro
  int erro = dx - dy;

  while (1) {
    putPixel(x0, y0, 250, 0, 0);

    // Quando a condicao for alcancada finaliza o loop
    if (x0 == x1 && y0 == y1) break;

    // atualiza o erro
    int erro2 = 2 * erro;

    if (erro2 > -dy) { // verifica se o erro esta acima
      erro -= dy;
      x0 += sx;
    }

    if (erro2 < dx) { // verifica se o erro esta abaixo
      erro += dx;
      y0 += sy;
    }
  }
}



int main(){

  // Limpar a imagem
  clearImage();

  // Executar o algoritmo DDA
  //drawBresenhamLinesIncomplete(0, 0, 200, 200);

  drawBresenhamLines(20, 20, 80, 20);
  drawBresenhamLines(20, 20, 20, 80);
  drawBresenhamLines(20, 80, 80, 80);
  drawBresenhamLines(80, 20, 80, 80);

  // Salvar a imagem em PPM
  saveImage();

  return 0;
}

Descrição do programa

Neste momento, estaríamos repetindo todo o processo descrito anteriormente. Para evitar redundância, descreveremos apenas o conteúdo que adicionamos ao arquivo. Sendo assim, falaremos sobre a função drawBresenhamLinesIncomplete. Esta função é descrita no texto Bresenham’s Algorithm.

void drawBresenhamLinesIncomplete( int x0, int y0, int x1, int y1 ){

  // calcula a variacao
  int dx = x1 - x0;
  int dy = y1 - y0;

  // calcula o erro
  int D = (2 * dy) - dx;

  int x = x0;
  int y = y0;

  putPixel(x, y, 255, 0, 0);

  while (x < x1){
    x = x + 1;
    if ( D < 0 ){
      D = D + (2 * dy);
    }
    else{
      y = y + 1;
      D = D + (2 * ( dy - dx ));
    }
    putPixel(x, y, 255, 0, 0);
  }

}

Na função drawBresenhamLines, incluimos todos os quadrantes como sugerido no artigo supracitado.

void drawBresenhamLines( int x0, int y0, int x1, int y1 ){
  // calcula a variacao absoluta
  int dx = abs(x1 - x0);
  int dy = abs(y1 - y0);

  // indica a direcao da reta
  int sx = (x0 < x1) ? 1 : -1; // direção de x
  int sy = (y0 < y1) ? 1 : -1; // direção de y

  // calcula o erro
  int erro = dx - dy;

  while (1) {
    putPixel(x0, y0, 250, 0, 0);

    // Quando a condicao for alcancada finaliza o loop
    if (x0 == x1 && y0 == y1) break;

    // atualiza o erro
    int erro2 = 2 * erro;

    if (erro2 > -dy) { // verifica se o erro esta acima
      erro -= dy;
      x0 += sx;
    }

    if (erro2 < dx) { // verifica se o erro esta abaixo
      erro += dx;
      y0 += sy;
    }
  }
}

Lecture 5

Nesta parte da disciplina apresentamos um algoritmo de preenchimento de triângulo usando interpolação de cores.

Coordenadas Baricêntricas

Sejam $C_0 = (x_0, y_0)$, $C_1 = (x_1, y_1)$ e $C_2 = (x_2, y_2)$ pontos não colineares no espaço 2D. Podemos realizar o preenchimento do polígono (triângulo) definido entre esses 3 pontos usando a equação: $C = \alpha C_0 + \beta C_1 + \gamma C_2$, onde $\alpha + \beta + \gamma = 1$.

Figure 8. Preenchimento de triângulos usando coordenadas baricêntricas

Código

A implementação do algoritmo de coordenadas baricêntricas está disponível no arquivo barycentric.c.

/**
 * \file barycentric.c
 *
 * \brief Implementação da renderizacao de modelo 3D
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Arido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date Jul 2025
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>

#define WIDTH 800
#define HEIGHT 800
#define MAX_VERTICES 50000
#define MAX_FACES 50000
#define MAX_FACE_VERTS 32

typedef struct {
  float x, y, z;
} Vertex;

typedef struct {
  int verts[MAX_FACE_VERTS];
  int n;
} Face;

unsigned char image[WIDTH][HEIGHT][3];

void set_pixel(int x, int y, unsigned char r, unsigned char g, unsigned char b) {
  if (x >= 0 && x < WIDTH && y >= 0 && y < HEIGHT) {
    image[y][x][0] = r;
    image[y][x][1] = g;
    image[y][x][2] = b;
  }
}

void draw_line(int x0, int y0, int x1, int y1) {
  for (float t = 0.0; t < 1.0; t = t + 0.0001)
    set_pixel((int)x0+(x1-x0)*t, (int)y0+(y1-y0)*t, 0, 0, 0);
}

void clr(){
  for(int i = 0; i < WIDTH; i++)
    for(int j = 0; j < HEIGHT; j++)
      for(int c = 0; c < 3; c++)
        image[i][j][c] = 255;
}

void save(){
  printf("P3\n %d \t %d\n 255\n", WIDTH, HEIGHT);
  for(int i = 0; i < WIDTH; i++){
    for(int j = 0; j < HEIGHT; j++){
      for(int c = 0; c < 3; c++){
        printf("%d \t", image[i][j][c]);
      }
      printf("\n");
    }
  }
}

int load_obj(const char *filename, Vertex *vertices, int *vcount, Face *faces,
             int *fcount) {
    FILE *file = fopen(filename, "r");
    if (!file) {
        perror("Erro ao abrir o arquivo");
        return 0;
    }

    char line[512];
    *vcount = 0;
    *fcount = 0;

    while (fgets(line, sizeof(line), file)) {
        if (strncmp(line, "v ", 2) == 0) {
            if (sscanf(line + 2, "%f %f %f", &vertices[*vcount].x,
                       &vertices[*vcount].y, &vertices[*vcount].z) == 3) {
                (*vcount)++;
            }
        } else if (strncmp(line, "f ", 2) == 0) {
            Face face = {.n = 0};
            char *token = strtok(line + 2, " \n");
            while (token && face.n < MAX_FACE_VERTS) {
                int index;
                if (sscanf(token, "%d", &index) == 1) {
                    face.verts[face.n++] = index;
                }
                token = strtok(NULL, " \n");
            }
            faces[(*fcount)++] = face;
        }
    }

    fclose(file);
    return 1;
}

void resizing( Vertex v0, Vertex v1 ){
  int x0 = (int)((v0.x + 1.0f) * WIDTH / 2.0f);
  int y0 = (int)((1.0f - v0.y) * HEIGHT / 2.0f);
  int x1 = (int)((v1.x + 1.0f) * WIDTH / 2.0f);
  int y1 = (int)((1.0f - v1.y) * HEIGHT / 2.0f);

  draw_line(x0, y0, x1, y1);
}


void render_faces(Vertex *vertices, Face *faces, int vcount, int fcount) {
  for (int i = 0; i < fcount; i++) {
    Face face = faces[i];
    for (int j = 0; j < face.n; j++) {
      Vertex v0 = vertices[face.verts[j] - 1];
      Vertex v1 = vertices[face.verts[(j + 1) % face.n] - 1];
      resizing(v0, v1);
    }
  }
}

void rotate_z(Vertex *v, float angle_rad) {
    float x = v->x;
    float y = v->y;
    v->x = x * cosf(angle_rad) - y * sinf(angle_rad);
    v->y = x * sinf(angle_rad) + y * cosf(angle_rad);
}

void project_3dto2d(Vertex *v) {
    v->x = (v->x + 1.0f) * (WIDTH  / 2.0f);
    v->y = (1.0f + v->y) * (HEIGHT / 2.0f);
}

void barycentric_coordinate( Vertex a, Vertex b, Vertex c, float red, float green, float blue ){
  // calculando o bounding box
  int x_min = floorf(fminf(fminf(a.x, b.x), c.x));
  int x_max = ceilf(fmaxf(fmaxf(a.x, b.x), c.x));
  int y_min = floorf(fminf(fminf(a.y, b.y), c.y));
  int y_max = ceilf(fmaxf(fmaxf(a.y, b.y), c.y));

  // Encontrando a Area do triangulo abc
  float area_abc = 0.5 * fabsf(a.x*(b.y - c.y) + b.x*(c.y - a.y) + c.x*(a.y - b.y));

  for (int y = y_min; y < y_max; y++){
    for (int x = x_min; x < x_max; x++){
      Vertex p = {x, y, 0};
      // Encontrando a Area dos triangulos
      float area_pbc = 0.5 * (p.x*(b.y - c.y) + b.x*(c.y - p.y) + c.x*(p.y - b.y));
      float area_apc = 0.5 * (a.x*(p.y - c.y) + p.x*(c.y - a.y) + c.x*(a.y - p.y));
      float area_abp = 0.5 * (a.x*(b.y - p.y) + b.x*(p.y - a.y) + p.x*(a.y - b.y));
      float alfa = area_pbc / area_abc;
      float beta = area_apc / area_abc;
      float gamma = area_abp / area_abc;
      if ( alfa >= 0.0 && beta >= 0.0 && gamma >= 0.0 ){
        set_pixel( x, y, red, green, blue );
      }
    }
  }
}

void render_faces_filled( Vertex *vertices, Face *faces, int vcount, int fcount){
  for (int i = 0; i < fcount; i++){
    Face face = faces[i];

    Vertex v0 = vertices[face.verts[0] - 1];
    Vertex v1 = vertices[face.verts[1] - 1];
    Vertex v2 = vertices[face.verts[2] - 1];

    // Rotacione os vertices (180 graus)
    rotate_z(&v0, M_PI);
    rotate_z(&v1, M_PI);
    rotate_z(&v2, M_PI);

    // Projecao 3D -> 2D
    project_3dto2d(&v0);
    project_3dto2d(&v1);
    project_3dto2d(&v2);

    barycentric_coordinate( v0, v1, v2, rand()%255, rand()%255, rand()%255 );
  }
}

int main(){

  Vertex vertices[MAX_VERTICES];
  Face faces[MAX_FACES];
  int vcount, fcount;

  clr();

  // Le o arquivo OBJ enviado
  if (!load_obj("models/wolf.obj", vertices, &vcount, faces, &fcount)) {
    return 1;
  }

  // Renderiza as faces no framebuffer
  render_faces_filled( vertices, faces, vcount, fcount );

  save();

  return 0;
}

Descrição do programa

Para evitar redundância, descreveremos apenas o conteúdo que adicionamos ao arquivo. Sendo assim, discutiremos sobre a função barycentric_coordinate. Esta função recebe 3 vértices e calcula o bounding box, ou seja, o volume que envolve o triângulo que desejamos preencher. Em seguida, encontramos as áreas dos triângulos e depois percorremos todos os pixels definido no bounding box com intuito de investigar se os alfa, beta e gamma são maiores ou iguais a zero para pintar o pixel.

void barycentric_coordinate( Vertex a, Vertex b, Vertex c ){
  // calculando o bounding box
  int x_min = floorf(fminf(fminf(a.x, b.x), c.x));
  int x_max = ceilf(fmaxf(fmaxf(a.x, b.x), c.x));
  int y_min = floorf(fminf(fminf(a.y, b.y), c.y));
  int y_max = ceilf(fmaxf(fmaxf(a.y, b.y), c.y));

  // Encontrando a área do triangulo abc
  float area_abc = 0.5 * fabsf(a.x*(b.y - c.y) + b.x*(c.y - a.y) + c.x*(a.y - b.y));
  float red = rand()%255;
  float green = rand()%255;
  float blue = rand()%255;
  for (int y = y_min; y < y_max; y++){
    for (int x = x_min; x < x_max; x++){
      Vertex p = {x, y, 0};
      // Encontrando a área dos triangulos
      float area_pbc = 0.5 * (p.x*(b.y - c.y) + b.x*(c.y - p.y) + c.x*(p.y - b.y));
      float area_apc = 0.5 * (a.x*(p.y - c.y) + p.x*(c.y - a.y) + c.x*(a.y - p.y));
      float area_abp = 0.5 * (a.x*(b.y - p.y) + b.x*(p.y - a.y) + p.x*(a.y - b.y));
      float alfa = area_pbc / area_abc;
      float beta = area_apc / area_abc;
      float gamma = area_abp / area_abc;
      if ( alfa >= 0.0 && beta >= 0.0 && gamma >= 0.0 ){
        set_pixel( x, y, red, green, blue );
      }
    }
  }
}

Uma outra função que devemos discutir é a função render_faces_filled. Nesta função, encontramos os 3 vértices para uma face de triângulo, transformamos esses vértices e preechemos esses triângulos usando a função barycentric_coordinate previamente discutida.

void render_faces_filled( Vertex *vertices, Face *faces, int vcount, int fcount){
  for (int i = 0; i < fcount; i++){
    Face face = faces[i];

    Vertex v0 = vertices[face.verts[0] - 1];
    Vertex v1 = vertices[face.verts[1] - 1];
    Vertex v2 = vertices[face.verts[2] - 1];

    // Rotacione os vertices (180 graus)
    rotate_z(&v0, M_PI);
    rotate_z(&v1, M_PI);
    rotate_z(&v2, M_PI);

    // Projecao 3D -> 2D
    project_3dto2d(&v0);
    project_3dto2d(&v1);
    project_3dto2d(&v2);

    barycentric_coordinate( v0, v1, v2 );
  }
}

Lecture 6

Vamos aprender como a iluminação é calculada em computação gráfica para simular a interação da luz com superfícies 3D.

Iluminação

A iluminação em computação gráfica simula como a luz interage com as superfícies dos objetos para gerar realismo visual. Os três principais componentes são: ambiente, que representa a luz difusa constante do ambiente; difusa, que depende do ângulo entre a luz e a superfície; e especular, que simula o brilho refletido em direção ao observador. Esses elementos compõem o modelo clássico de Phong, amplamente usado por seu equilíbrio entre realismo e eficiência. A intensidade final da cor é calculada somando essas contribuições, considerando também os materiais e a direção da câmera.

Figure 9. Resultado da iluminação de Phong

Reflexão ambiente

$I_{amb} = k_a I_{ambiente}$

$k_a$: coeficiente de reflexão ambiente do material (0 a 1);
$I_{ambiente}$: intensidade da luz ambiente

Reflexão difusa (Lambert)

$I_{diff} = k_d I_L max(0, \vec{N} . \vec{L})$

$k_d$: coeficiente de reflexão difuso;
$I_{L}$: intensidade da luz;
$\vec{N}$: vetor normal da superfície;
$\vec{L}$: vetor da direção da luz
produto escalar: mede o "alinhamento" da luz com a superfície

Reflexão especular (Phong)

$I_{spec} = k_s I_L max(0, \vec{R} . \vec{V})^n$, onde $\vec{R} = 2(\vec{N}.\vec{L})\vec{N} - \vec{L}$

$k_s$: coeficiente especular;
$I_{L}$: intensidade da luz;
$\vec{R}$: vetor de reflexão da luz;
$\vec{V}$: vetor em direção à câmera
$n$: brilho (quanto maior, mais estreito o brilho)

Código

A implementação da iluminação está disponível no arquivo light.c.

/**
 * \file light.c
 *
 * \brief Implementação da iluminação com reflexão ambiente, difusa (lambert)
 * e especular (phong)
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Arido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date Jul 2025
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>

#define WIDTH 800
#define HEIGHT 800
#define MAX_VERTICES 50000
#define MAX_FACES 50000
#define MAX_FACE_VERTS 32

typedef struct {
  float x, y, z;
} Vertex;

typedef struct {
  int verts[MAX_FACE_VERTS];
  int n;
} Face;

unsigned char image[WIDTH][HEIGHT][3];

void set_pixel(int x, int y, unsigned char r, unsigned char g, unsigned char b) {
  if (x >= 0 && x < WIDTH && y >= 0 && y < HEIGHT) {
    image[y][x][0] = r;
    image[y][x][1] = g;
    image[y][x][2] = b;
  }
}

void draw_line(int x0, int y0, int x1, int y1) {
  for (float t = 0.0; t < 1.0; t = t + 0.0001)
    set_pixel((int)x0+(x1-x0)*t, (int)y0+(y1-y0)*t, 0, 0, 0);
}

void clr(){
  for(int i = 0; i < WIDTH; i++)
    for(int j = 0; j < HEIGHT; j++)
      for(int c = 0; c < 3; c++)
        image[i][j][c] = 255;
}

void save(){
  printf("P3\n %d \t %d\n 255\n", WIDTH, HEIGHT);
  for(int i = 0; i < WIDTH; i++){
    for(int j = 0; j < HEIGHT; j++){
      for(int c = 0; c < 3; c++){
        printf("%d \t", image[i][j][c]);
      }
      printf("\n");
    }
  }
}

int load_obj(const char *filename, Vertex *vertices, int *vcount, Face *faces,
             int *fcount) {
    FILE *file = fopen(filename, "r");
    if (!file) {
        perror("Erro ao abrir o arquivo");
        return 0;
    }

    char line[512];
    *vcount = 0;
    *fcount = 0;

    while (fgets(line, sizeof(line), file)) {
        if (strncmp(line, "v ", 2) == 0) {
            if (sscanf(line + 2, "%f %f %f", &vertices[*vcount].x,
                       &vertices[*vcount].y, &vertices[*vcount].z) == 3) {
                (*vcount)++;
            }
        } else if (strncmp(line, "f ", 2) == 0) {
            Face face = {.n = 0};
            char *token = strtok(line + 2, " \n");
            while (token && face.n < MAX_FACE_VERTS) {
                int index;
                if (sscanf(token, "%d", &index) == 1) {
                    face.verts[face.n++] = index;
                }
                token = strtok(NULL, " \n");
            }
            faces[(*fcount)++] = face;
        }
    }

    fclose(file);
    return 1;
}

void rotate_z(Vertex *v, float angle_rad) {
    float x = v->x;
    float y = v->y;
    v->x = x * cosf(angle_rad) - y * sinf(angle_rad);
    v->y = x * sinf(angle_rad) + y * cosf(angle_rad);
}

void project_3dto2d(Vertex *v) {
    v->x = (v->x + 1.0f) * (WIDTH  / 2.0f);
    v->y = (1.0f + v->y) * (HEIGHT / 2.0f);
}

void barycentric_coordinate( Vertex a, Vertex b, Vertex c, float red, float green, float blue ){
  // calculando o bounding box
  int x_min = floorf(fminf(fminf(a.x, b.x), c.x));
  int x_max = ceilf(fmaxf(fmaxf(a.x, b.x), c.x));
  int y_min = floorf(fminf(fminf(a.y, b.y), c.y));
  int y_max = ceilf(fmaxf(fmaxf(a.y, b.y), c.y));

  // Encontrando a área do triangulo abc
  float area_abc = 0.5 * fabsf(a.x*(b.y - c.y) + b.x*(c.y - a.y) + c.x*(a.y - b.y));

  for (int y = y_min; y <= y_max; y++){
    for (int x = x_min; x <= x_max; x++){
      Vertex p = {x, y, 0};
      // Encontrando a área dos triangulos
      float area_pbc = 0.5 * (p.x*(b.y - c.y) + b.x*(c.y - p.y) + c.x*(p.y - b.y));
      float area_apc = 0.5 * (a.x*(p.y - c.y) + p.x*(c.y - a.y) + c.x*(a.y - p.y));
      float area_abp = 0.5 * (a.x*(b.y - p.y) + b.x*(p.y - a.y) + p.x*(a.y - b.y));
      float alfa = area_pbc / area_abc;
      float beta = area_apc / area_abc;
      float gamma = area_abp / area_abc;
      if ( alfa >= 0.0 && beta >= 0.0 && gamma >= 0.0 ){
        set_pixel( x, y, red, green, blue );
      }
    }
  }
}

Vertex sub( Vertex a, Vertex b ){
  return (Vertex) {a.x - b.x, a.y - b.y, a.z - b.z};
}

float dot( Vertex a, Vertex b ){
  return a.x * b.x + a.y * b.y + a.z * b.z;
}

Vertex cross( Vertex a, Vertex b ){
  return (Vertex) {a.y*b.z - a.z*b.y, a.z*b.x - a.x*b.z, a.x*b.y - a.y*b.x};
}

Vertex normalize( Vertex v ){
  float len = sqrtf(v.x*v.x + v.y*v.y + v.z*v.z);
  if ( len == 0 ) return (Vertex){0, 0, 0};
  return (Vertex){v.x/len, v.y/len, v.z/len};
}

Vertex scalar( float x, Vertex v ){
  return (Vertex){ x*v.x, x*v.y, x*v.z };
}

void render_faces_filled( Vertex *vertices, Face *faces, int vcount, int fcount ){

  Vertex light = {0, 0, -1}; //{0.25, 0.0, -0.75};
  Vertex view_dir = {0, 0, 1}; // Camera olhando para -z

  for (int i = 0; i < fcount; i++){
    Face face = faces[i];

    Vertex v0 = vertices[face.verts[0] - 1];
    Vertex v1 = vertices[face.verts[1] - 1];
    Vertex v2 = vertices[face.verts[2] - 1];

    // Vetor normal
    Vertex v1_v0 = sub( v1, v0 );
    Vertex v2_v0 = sub( v2, v0 );
    Vertex normal = normalize( cross( v2_v0, v1_v0 ) );

    // Coeficientes de phong
    float ka = 0.2; // ambiente
    float kd = 0.6; // difusa
    float ks = 0.4; // especular
    int brilho = 32;

    // Normalizar luz e direcao da camera
    Vertex L = normalize(light);
    Vertex V = normalize(view_dir);

    // Iluminacao difusa
    float diff = fmaxf(0, dot( normal, L ));

    // Iluminacao especular
    Vertex R = sub( scalar(2.0 * dot(normal,L), normal), L); // R = 2(N.L)N - L
    float spec = powf(fmaxf(0, dot(R, V)), brilho);

    // Intensidade final
    float intensity = ka + kd * diff + ks * spec;
    if ( intensity > 1.0 ) intensity = 1.0;

    // Rotacione os vertices (180 graus)
    rotate_z(&v0, M_PI);
    rotate_z(&v1, M_PI);
    rotate_z(&v2, M_PI);

    // Projecao 3D -> 2D
    project_3dto2d(&v0);
    project_3dto2d(&v1);
    project_3dto2d(&v2);

    barycentric_coordinate( v0, v1, v2, intensity*255, intensity*255, intensity*255 );
  }
}

int main(){

  Vertex vertices[MAX_VERTICES];
  Face faces[MAX_FACES];
  int vcount, fcount;

  clr();

  // Lê o arquivo OBJ enviado
  if (!load_obj("models/wolf.obj", vertices, &vcount, faces, &fcount)) {
    return 1;
  }

  // Renderiza as faces no framebuffer
  render_faces_filled( vertices, faces, vcount, fcount );

  save();

  return 0;
}

Descrição do programa

Neste código, implementamos funções auxiliares para o cálculo da iluminação, como subtração de vetores (sub), produto escalar (dot), produto vetorial (cross), normalização (normalize) e multiplicação por escalar (scalar). Essas funções são utilizadas na função render_faces_filled, responsável por aplicar o modelo de iluminação sobre os triângulos da malha. A partir dos vertices $v0$, $v1$ e $v2$ de cada triângulo, calculamos a normal da face e definimos os coeficientes de iluminação. Em seguida, normalizamos os vetores da luz e do observador, computamos as componentes difusa e especular, e combinamos os resultados para determinar a intensidade final da cor em cada triângulo renderizado.

void render_faces_filled( Vertex *vertices, Face *faces, int vcount, int fcount ){

  Vertex light = {0, 0, -1}; //{0.25, 0.0, -0.75};
  Vertex view_dir = {0, 0, 1}; // Camera olhando para -z

  for (int i = 0; i < fcount; i++){
    Face face = faces[i];

    Vertex v0 = vertices[face.verts[0] - 1];
    Vertex v1 = vertices[face.verts[1] - 1];
    Vertex v2 = vertices[face.verts[2] - 1];

    // Vetor normal
    Vertex v1_v0 = sub( v1, v0 );
    Vertex v2_v0 = sub( v2, v0 );
    Vertex normal = normalize( cross( v2_v0, v1_v0 ) );

    // Coeficientes de phong
    float ka = 0.2; // ambiente
    float kd = 0.6; // difusa
    float ks = 0.4; // especular
    int brilho = 32;

    // Normalizar luz e direcao da camera
    Vertex L = normalize(light);
    Vertex V = normalize(view_dir);

    // Iluminacao difusa
    float diff = fmaxf(0, dot( normal, L ));

    // Iluminacao especular
    Vertex R = sub( scalar(2.0 * dot(normal,L), normal), L); // R = 2(N.L)N - L
    float spec = powf(fmaxf(0, dot(R, V)), brilho);

    // Intensidade final
    float intensity = ka + kd * diff + ks * spec;
    if ( intensity > 1.0 ) intensity = 1.0;

    // Rotacione os vertices (180 graus)
    rotate_z(&v0, M_PI);
    rotate_z(&v1, M_PI);
    rotate_z(&v2, M_PI);

    // Projecao 3D -> 2D
    project_3dto2d(&v0);
    project_3dto2d(&v1);
    project_3dto2d(&v2);

    barycentric_coordinate( v0, v1, v2, intensity*255, intensity*255, intensity*255 );
  }
}

Lecture 7

Vamos compreender como a técnica ray tracing funciona.

Ray Tracing

Técnica de síntese de imagens fotorealísticas que traça raios da câmera até a cena. Se um raio intercepta algum objeto da cena, cálculos relacionados a iluminação são realizados. Caso contrário, a cor do background é retornado.

Figure 10. Imagens sintetizadas a partir do algoritmo raytracing.

Códigos

A implementação das imagens estão disponiveis nos arquivos raytracing.c, raytracing2.c e raytracing3.c, respectivamente.

Renderização de uma esfera com background azul

/**
 * \file raytracing.c
 *
 * \brief Implementação do traçador de raios para criação de imagens
 * com renderização de uma esfera.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Arido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date Jul 2025
 */

#include <stdio.h>
#include <math.h>

#define WIDTH 800
#define HEIGHT 600

unsigned char img[WIDTH][HEIGHT][3];

typedef struct{
  float x, y, z;
} Vertex;

Vertex add( Vertex a, Vertex b ){ return (Vertex){a.x + b.x, a.y + b.y, a.z + b.z}; }
Vertex sub( Vertex a, Vertex b ){ return (Vertex){a.x - b.x, a.y - b.y, a.z - b.z}; }
Vertex scale( Vertex v, float s ){ return (Vertex){s*v.x, s*v.y, s*v.z}; }
float dot(Vertex a, Vertex b){ return a.x*b.x + a.y*b.y + a.z*b.z; }
float length(Vertex v){ return sqrtf(dot(v, v)); }
Vertex normalize( Vertex v ){ return scale(v, 1.0f / length( v )); }

void save(){
  printf("P3\n %d \t %d\n 255\n", WIDTH, HEIGHT);
  for (int y = 0; y < HEIGHT; y++){
    for (int x = 0; x < WIDTH; x++){
      for (int c = 0; c < 3; c++){
        printf("%d \t", img[x][y][c]);
      }
      printf("\n");
    }
  }
}

// Retorna t (distância) ou -1 se não há interseção
float intersecao_esfera( Vertex O, Vertex D, Vertex C, float r ){
  Vertex L = sub( O, C );
  float a = dot( D, D );
  float b = 2.0 * dot(L, D);
  float c = dot(L, L) - r * r;
  float delta = b * b - 4 * a * c;
  if ( delta < 0 ) return -1.0;
  float sqrt_delta = sqrtf( delta );
  float t0 = (-b - sqrt_delta) / (2 * a);
  float t1 = (-b + sqrt_delta) / (2 * a);
  if ( t0 > 0.001 ) return t0;
  if ( t1 > 0.001 ) return t1;
  return -1.0;
}

void render(){
  Vertex camera = (Vertex){0, 0, 0};
  Vertex C = (Vertex){0, 0, -5};
  float r = 1.0;
  Vertex light_position = normalize( (Vertex){1, 1, 1} );

  for (int y = 0; y < HEIGHT; y++){
    for (int x = 0; x < WIDTH; x++){
      float fx = (2.0 * x / WIDTH - 1.0) * (float)WIDTH / HEIGHT;
      float fy = 1.0 - 2.0 * y / (float) HEIGHT;
      Vertex D = normalize( (Vertex){fx, fy, -1} );

      float t = intersecao_esfera(camera, D, C, r);
      if ( t > 0.0 ){
        Vertex hitPoint = add( camera, scale( D, t ));
        Vertex normal = normalize( sub(hitPoint, C) );
        float diff = fmaxf(0.0, dot(normal, light_position));
        img[x][y][0] = (unsigned char)(diff * 255);
        img[x][y][1] = 0;
        img[x][y][2] = 0;
      }
      else{
        img[x][y][0] = 135;
        img[x][y][1] = 206;
        img[x][y][2] = 250;
      }
    }
  }
}

int main(){
  render();
  save();
  return 0;
}

Renderização de uma esfera com plano xadrez

/**
 * \file raytracing2.c
 *
 * \brief Implementação do traçador de raios para criação de imagens
 * com renderização de uma esfera e um plano.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Arido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date Jul 2025
 */

#include <stdio.h>
#include <math.h>

#define WIDTH 800
#define HEIGHT 600

unsigned char img[WIDTH][HEIGHT][3];

typedef struct{
  float x, y, z;
} Vertex;

Vertex add( Vertex a, Vertex b ){ return (Vertex){a.x + b.x, a.y + b.y, a.z + b.z}; }
Vertex sub( Vertex a, Vertex b ){ return (Vertex){a.x - b.x, a.y - b.y, a.z - b.z}; }
Vertex scale( Vertex v, float s ){ return (Vertex){s*v.x, s*v.y, s*v.z}; }
float dot(Vertex a, Vertex b){ return a.x*b.x + a.y*b.y + a.z*b.z; }
float length(Vertex v){ return sqrtf(dot(v, v)); }
Vertex normalize( Vertex v ){ return scale(v, 1.0f / length( v )); }

void save(){
  printf("P3\n %d \t %d\n 255\n", WIDTH, HEIGHT);
  for (int y = 0; y < HEIGHT; y++){
    for (int x = 0; x < WIDTH; x++){
      for (int c = 0; c < 3; c++){
        printf("%d \t", img[x][y][c]);
      }
      printf("\n");
    }
  }
}

// Retorna t (distância) ou -1 se não há interseção
float intersecao_esfera( Vertex O, Vertex D, Vertex C, float r ){
  Vertex L = sub( O, C );
  float a = dot( D, D );
  float b = 2.0 * dot(L, D);
  float c = dot(L, L) - r * r;
  float delta = b * b - 4 * a * c;
  if ( delta < 0 ) return -1.0;
  float sqrt_delta = sqrtf( delta );
  float t0 = (-b - sqrt_delta) / (2 * a);
  float t1 = (-b + sqrt_delta) / (2 * a);
  if ( t0 > 0.001 ) return t0;
  if ( t1 > 0.001 ) return t1;
  return -1.0;
}

// Retorna t (distância) ou -1 se não há interseção
float intersecao_plano(Vertex O, Vertex D, Vertex P, Vertex N){
  float denominador = dot( N, D );
  if ( fabs(denominador) < 0.0 ) return -1.0;
  float t = dot( sub(P, O), N ) / denominador;
  return ( t > 0.0 ) ? t : -1.0;
}

void render(){
  Vertex camera = (Vertex){0, 0, 0};
  Vertex light_position = normalize( (Vertex){1, 1, 1} );

  // Parâmetros da esfera
  Vertex C = (Vertex){0, 0, -5};
  float r = 1.0;

  // Parâmetros do plano
  Vertex ponto_plano = (Vertex){0, -1, 0};
  Vertex normal_plano = (Vertex){0, 1, 0};


  for (int y = 0; y < HEIGHT; y++){
    for (int x = 0; x < WIDTH; x++){
      float fx = (2.0 * x / WIDTH - 1.0) * (float)WIDTH / HEIGHT;
      float fy = 1.0 - 2.0 * y / (float) HEIGHT;
      Vertex D = normalize( (Vertex){fx, fy, -1} );

      float ts = intersecao_esfera(camera, D, C, r);
      float tp = intersecao_plano(camera, D, ponto_plano, normal_plano);

      if ( ts > 0.0 && (tp < 0 || ts < tp) ){
        Vertex hitPoint = add( camera, scale( D, ts ));
        Vertex normal = normalize( sub(hitPoint, C) );
        float diff = fmaxf(0.0, dot(normal, light_position));
        img[x][y][0] = (unsigned char)(diff * 255);
        img[x][y][1] = 0;
        img[x][y][2] = 0;
      }
      else{
        if ( tp > 0 ){
          Vertex hitPoint = add( camera, scale( D, tp ) );
          // Criar um xadrez
          float xadrez = ((int)(floor(hitPoint.x) + floor(hitPoint.z))) % 2;
          // Quando xadrez for par imprime mais claro e quando for ímpar mais escuro
          unsigned char c = xadrez ? 155 : 80;
          float diff = fmaxf(0.0, dot(normal_plano, light_position));
          img[x][y][0] = c;
          img[x][y][1] = c;
          img[x][y][2] = c;
        }
        else{
          img[x][y][0] = 135;
          img[x][y][1] = 206;
          img[x][y][2] = 250;
        }
      }
    }
  }
}

int main(){
  render();
  save();
  return 0;
}

Renderização de uma esfera com plano e reflexão especular

/**
 * \file raytracing3.c
 *
 * \brief Implementação do traçador de raios para criação de imagens
 * com renderização de uma esfera e um plano. Além disso, implementamos
 * a reflexão.
 *
 * \author
 * Petrucio Ricardo Tavares de Medeiros \n
 * Universidade Federal Rural do Semi-Arido \n
 * Departamento de Engenharias e Tecnologia \n
 * petrucio at ufersa (dot) edu (dot) br
 *
 * \version 1.0
 * \date Jul 2025
 */

#include <stdio.h>
#include <math.h>

#define WIDTH 800
#define HEIGHT 600

#define MAX_DEPTH 2

unsigned char img[WIDTH][HEIGHT][3];

typedef struct{
  float x, y, z;
} Vertex;

Vertex add( Vertex a, Vertex b ){ return (Vertex){a.x + b.x, a.y + b.y, a.z + b.z}; }
Vertex sub( Vertex a, Vertex b ){ return (Vertex){a.x - b.x, a.y - b.y, a.z - b.z}; }
Vertex scale( Vertex v, float s ){ return (Vertex){s*v.x, s*v.y, s*v.z}; }
float dot(Vertex a, Vertex b){ return a.x*b.x + a.y*b.y + a.z*b.z; }
float length(Vertex v){ return sqrtf(dot(v, v)); }
Vertex normalize( Vertex v ){ return scale(v, 1.0f / length( v )); }
Vertex reflect(Vertex D, Vertex N){ return sub(D, scale(N, 2.0f * dot(D, N))); }

void save(){
  printf("P3\n %d \t %d\n 255\n", WIDTH, HEIGHT);
  for (int y = 0; y < HEIGHT; y++){
    for (int x = 0; x < WIDTH; x++){
      for (int c = 0; c < 3; c++){
        printf("%d \t", img[x][y][c]);
      }
      printf("\n");
    }
  }
}

// Retorna t (distância) ou -1 se não há interseção
float intersecao_esfera( Vertex O, Vertex D, Vertex C, float r ){
  Vertex L = sub( O, C );
  float a = dot( D, D );
  float b = 2.0 * dot(L, D);
  float c = dot(L, L) - r * r;
  float delta = b * b - 4 * a * c;
  if ( delta < 0 ) return -1.0;
  float sqrt_delta = sqrtf( delta );
  float t0 = (-b - sqrt_delta) / (2 * a);
  float t1 = (-b + sqrt_delta) / (2 * a);
  if ( t0 > 0.001 ) return t0;
  if ( t1 > 0.001 ) return t1;
  return -1.0;
}

// Retorna t (distância) ou -1 se não há interseção
float intersecao_plano(Vertex O, Vertex D, Vertex P, Vertex N){
  float denominador = dot( N, D );
  if ( fabs(denominador) < 0.0 ) return -1.0;
  float t = dot( sub(P, O), N ) / denominador;
  return ( t > 0.0 ) ? t : -1.0;
}

Vertex trace(Vertex O, Vertex D, int depth){
  Vertex light_position = normalize( (Vertex){1, 1, 1} );

  // Parâmetros da esfera
  Vertex C = (Vertex){0, 0, -5};
  float r = 1.0;

  // Parâmetros do plano
  Vertex ponto_plano = (Vertex){0, -1, 0};
  Vertex normal_plano = (Vertex){0, 1, 0};

  float ts = intersecao_esfera(O, D, C, r);
  float tp = intersecao_plano(O, D, ponto_plano, normal_plano);

  if ( ts > 0.0 && (tp < 0 || ts < tp) ){
    Vertex hitPoint = add( O, scale( D, ts ));
    Vertex normal = normalize( sub(hitPoint, C) );
    float diff = fmaxf(0.0, dot(normal, light_position));

    // Cor difusa
    Vertex cor = scale((Vertex){255, 0, 0}, diff);

    // Reflexão
    if ( depth < MAX_DEPTH ){
      Vertex refl_dir = normalize(reflect(D, normal));
      Vertex refl_color = trace(add(hitPoint, scale(normal, 1e-4)), refl_dir, depth + 1);
      cor = add(scale(cor, 0.5f), scale(refl_color, 0.5f));
    }
    return cor;
  }
  else{
    if ( tp > 0 ){
      Vertex hitPoint = add( O, scale( D, tp ) );
      // Criar um xadrez
      float xadrez = ((int)(floor(hitPoint.x) + floor(hitPoint.z))) % 2;
      // Quando xadrez for par imprime mais claro e quando for ímpar mais escuro
      unsigned char c = xadrez ? 155 : 80;
      float diff = fmaxf(0.0, dot(normal_plano, light_position));
      return (Vertex){c, c, c};
    }
    else{
      return (Vertex){135, 206, 250}; // fundo azul claro
    }
  }
}

void render(){
  Vertex camera = (Vertex){0, 0, 0};

  for (int y = 0; y < HEIGHT; y++){
    for (int x = 0; x < WIDTH; x++){
      float fx = (2.0 * x / WIDTH - 1.0) * (float)WIDTH / HEIGHT;
      float fy = 1.0 - 2.0 * y / (float) HEIGHT;
      Vertex D = normalize( (Vertex){fx, fy, -1} );
      Vertex color = trace(camera, D, 0);
      img[x][y][0] = (unsigned char)color.x;
      img[x][y][1] = (unsigned char)color.y;
      img[x][y][2] = (unsigned char)color.z;
    }
  }
}

int main(){
  render();
  save();
  return 0;
}